As I was falling asleep one night I began to think about regular polygons inscribed in the unit circle. I imagined adding more and more sides to the polygon and watching as the area of the polygon approached the area of the circle. I wondered how to calculate the ratio of the area of the polygon to the circle, and what the curve would look like if I were to plot the values for increasing numbers of sides. I wondered about similar plots for polygons circumscribing the unit circle. I understood that for large numbers of sides the ratio of the areas between the polygon and the circle would approach one, and likewise the ratio of the areas between the inscribed and circumscribed polygons would approach one, albeit more slowly as the circumscribed polygon will always be larger than the unit circle. Would the approach to one be symmetric for the case of the inscribed versus the circumscribed polygon?

Inscribed Polygons

I realized calculating the area of a regular polygon with $n$ sides inscribed in the unit circle should be fairly straightforward since any regular polygon can be divided into $n$ isosceles triangles sharing a common vertex at the center of the polygon. In this case the equal sides of the triangle have a length of one. Also all of the angles are known, since the interior angle must be $2\pi/n$ .

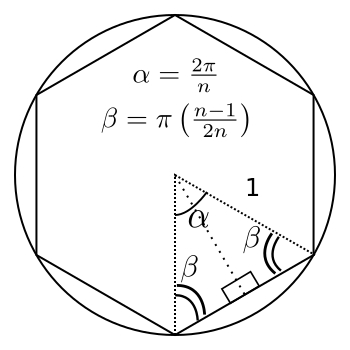
The triangle can be divided into two right triangles whose non-right angles are $\alpha / 2$ and $\beta$ , and each hypotenuse has a length of one. The area of each right triangle is shown to be

$\begin{aligned} A &= \frac{1}{2}\sin\left(\frac{\pi}{2}\left(\frac{n-2}{n}\right)\right) \cos\left(\frac{\pi}{2}\left(\frac{n-2}{n}\right)\right) \\ &= \frac{1}{2}\sin\left(\frac{\pi}{2} - \frac{\pi}{n}\right) \cos\left(\frac{\pi}{2} - \frac{\pi}{n}\right) \\ &= \frac{1}{2}\cos\left(\frac{\pi}{2}\right)\sin\left(\frac{\pi}{2}\right) \\ &= \frac{1}{4}\sin\left(\frac{2\pi}{n}\right) \end{aligned}$

In total there are $2n$ of these triangles per polygon, so the total area of the inscribed polygon, $A^I_n \equiv 2An$ , is therefore

$\label{inscribe} A^I_n = \frac{n}{2}\sin\left(\frac{2\pi}{n}\right)$

Circumscribed Polygons

The same procedure as before for calculating area applies to a regular polygon circumscribing the unit circle.

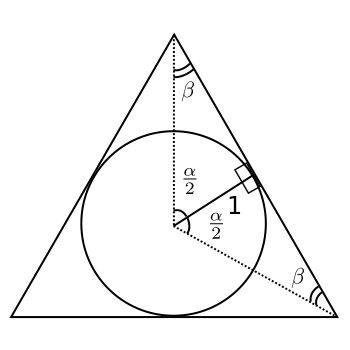
Finding the area of the right triangle is trivial in this case as the base is just the radius of the unit circle and the height is the tangent of $\alpha / 2$ . Therefore the area of each right triangle is $\tan(\pi /n)/2$ . Since there are $2n$ such triangles the total area of the polgon is

$\label{circumscribe} A^C_n = n\, \tan\left(\frac{\pi}{n}\right)$

Ratio of Areas

I’m interested in the ratio of the area of the polygon to that of the unit circle and seeing how the ratio changes with various values of $n$ . Dividing the equations for the inscribed area and the circumscribed area by the area of the unit circle, $\pi$ , and treating them as functions of $n$ , we get

$A_I(n) = \frac{n}{2\pi} \sin\left(\frac{2\pi}{n}\right)$
$A_C(n) = \frac{n}{\pi} \tan\left(\frac{\pi}{n}\right)$

I’m also interested in the ratio of the area of the inscribed polygon to the circumscribed polygon, as this will approach 1 for large $n$ just as the previous two equations.

$A_{I/C}(n) \equiv \frac{A_I(n)}{A_C(n)} = \frac{\sin\left(\frac{2\pi}{n}\right)}{2\, \tan\left(\frac{\pi}{n}\right)}$

The following figure shows a plot of each function for values from 3 to 30.

It’s clear from the plot that $A_I(n)$ and $A_C(n)$ are not symmetric about 1 and that the ratio of the areas of the polygons converges more slowly than the other two functions. However it’s not intuitively clear to me from the ratio equations that the plots should have the shape that they do.

In an attempt to get a simpler explanation of the shape of the curves the ratio functions can be expanded into the first few terms of their respective Taylor series.

$\begin{aligned} A_I(n) &= \frac{n}{2\pi} \sin\left(\frac{2\pi}{n}\right) \\ &= \frac{n}{2\pi} \left[\frac{2\pi}{n} - \frac{1}{6}{\left(\frac{2\pi}{n}\right)}^3 + \frac{1}{120}{\left(\frac{2\pi}{n}\right)}^5 + \dots\right] \\ &= \frac{n}{2\pi} \left[\frac{2\pi}{n} - \frac{1}{6}{\left(\frac{2\pi}{n}\right)}^3 + \mathcal{O}{\left(\frac{2\pi}{n}\right)}^5\right] \\ &\approx 1 - \frac{2\pi^2}{3n^2} \end{aligned}$

$\begin{aligned} A_C(n) &= \frac{n}{\pi} \sin\left(\frac{2\pi}{n}\right) \\ &= \frac{n}{\pi} \left[\frac{\pi}{n} - \frac{1}{3}{\left(\frac{\pi}{n}\right)}^3 + \frac{2}{15}{\left(\frac{\pi}{n}\right)}^5 + \dots\right] \\ &= \frac{n}{\pi} \left[\frac{\pi}{n} - \frac{1}{3}{\left(\frac{\pi}{n}\right)}^3 + \mathcal{O}{\left(\frac{\pi}{n}\right)}^5\right] \\ &\approx 1 + \frac{\pi^2}{3n^2} \end{aligned}$

The ratio between $A_I(n)$ and $A_C(n)$ is a little bit trickier but we can still eliminate higher order terms for an approximation.

$A_{I/C}(n) \approx \frac{1 - \frac{2\pi^2}{3n^2}}{1 + \frac{\pi^2}{3n^2}}$

For clarity let $x \equiv \frac{\pi^2}{3n^2}$ .

$\begin{aligned} A_{I/C}(n) &\approx \frac{1-2x}{1+x} \\ &\approx \frac{1-2x}{1+x}\cdot\frac{1-x}{1-x} \\ &\approx \frac{2x^2-3x+1}{1-x^2} \\ &\approx \frac{1-3x+\mathcal{O}{\left(x\right)}^2}{1-\mathcal{O}{\left(x\right)}^2} \\ &\approx 1-3x \\ &\approx 1-\frac{\pi^2}{n^2} \end{aligned}$

Finally we arrive at a set of approximate ratio equations that clearly show the trends in the plot.

$\begin{aligned} A_I(n) &\approx 1 - \frac{2\pi^2}{3n^2} \\ A_C(n) &\approx 1 + \frac{\pi^2}{3n^2} \\ A_{I/C}(n) &\approx 1-\frac{\pi^2}{n^2} \end{aligned}$

They show that $A_I(n)$ and $A_C(n)$ are not symmetric around 1 and that $A_{I/C}(n)$ has the shallowest approach toward the asymptote.

One thought on “Regular Polygons and the Unit Circle”

Jessica Cruickshank

2 thoughts – 1. I love that this is what was rolling around in your brain as you were trying to fall asleep. #nerdsunite! 2. The header photograph is the best. Hope you are well.

LikeLike

October 31, 2016 at 10:33 am Reply

Vernon W. Miller

Regular Polygons and the Unit Circle

Inscribed Polygons

Circumscribed Polygons

Ratio of Areas

One thought on “Regular Polygons and the Unit Circle”

Leave a comment Cancel reply

Inscribed Polygons

Circumscribed Polygons

Ratio of Areas

Share this:

One thought on “Regular Polygons and the Unit Circle”

Leave a comment Cancel reply